ランチェスターの法則とは?弱者が強者に勝つヒントになります。

「ブログにも応用できるの?」
この記事は、この様な方へ向けて書いています。
網羅的に情報を書きますが、分かりやすい内容であると思います。
この記事を読むことで得られる知識
- ランチェスターの法則の概要
- ランチェスターの法則の計算式まで理解
- ランチェスター戦略の概要
- マーケティングに活かす方法
※少し専門的な内容になるため、ゆっくりとお読み下さい。
では、記事内容へ入ります。
ランチェスターの法則とは?

ランチェスターの法則とは、戦争において「兵士の減少する度合い」を数理モデルで表したものです。
数理モデルとは、「何かの現象を簡略化して捉え、数式で表したもの」です。
ランチェスターさんは、戦争での戦略を考える為に、数式で戦闘結果を予想できないか考えた結果、「兵士の減少数」に近似する式を導き出したのです。
これにより、「何人くらいが生き残り」「どちらが勝つか」を予想することが可能となりました。

2つの法則から成り立つ

ランチェスターの法則は、2つの法則から成り立ちます。
それは、
- 第一法則
- 第二法則
この2つの法則です。それぞれについて記述します。
ランチェスターの法則「第一法則」(弱者の戦略)

第一法則は、「弱者のための法則」とも言われています。
どの様な法則かというと、「剣や槍などの近距離戦」で当てはまる法則です。一騎打ちの法則とも呼ばれます。近距離戦ですね。
武器の性能が同じだった場合、「Aが20人残して勝利」します。
具体的な数式を使った詳しい解説は後々するのですが、簡単な数式っぽいものを挙げると、
大体どの戦いもこの式に近似するため、戦争の勝敗、被害の大小が予測できます。
第一法則はマーケティングにどう活かす?
マーケティングに第一法則のどこを活かすか?というと、基本的に「兵力が大きい相手とは戦わない。」というところです。
大企業と同じジャンルで同じ様な製品を投入しても、たとえ一時的に製品レベルが上回ったとしても、そのアイデアを模倣した上位互換の製品をすぐに作って、市場に投入されてしまいます。
「真っ向勝負では勝ち目がない」ことを意味します。
では、どう戦うのか?
について解説していきます。
差別化 or 一点集中

「真っ向勝負しない」というだけで、戦い方があります。
それは、
- 差別化する(共存する)
- 集中して攻撃して一点突破する
この2つが挙げられます。「ランチェスター戦略」ですね。
差別化
1つ目は、大企業が相手にしない様な小さい市場を見つけて攻めることが大切です。
同じ様な製品・サービスを作るにしても、大企業が満たしている「本質サービス」とは少しずれたニーズを満たすことで「差別化」をすることが重要です。
「本質サービス」については、下記の記事の途中で解説しています。
マーケティングの基本的な考え方、そのプロセスとは?【図あり】
一点集中
2つ目は、「集中して攻撃して一点突破する」という方法です。トータルの経営資源は少なくても、その全てを一点に集中させれば、勝つ可能性があがります。
具体例を挙げると、
また、函館市のファーストフード店舗数は、
1位 ラッキーピエロ
2位 マクドナルド
3位 ケンタッキーフライドチキン
この様に、なっていて、他のハンバーガー店にとどまらず絶大な人気を博しています!
これらを上手く活かすと、自社よりも「資本」「社員数」などが勝っている格上企業に、勝つことができます!

歴史から学ぶ

自分達が優勢な状況が訪れるまで動き回り、機会をうかがいました。これによって相手が分散し少数になっている所に、大群で攻めて、トータルの兵士の人数では劣っていても勝つことができ功績を残しました。
重要な拠点 < 有利な陣地
「賢者は歴史から学び、愚者は経験から学ぶ。」とも言いますからね。歴史からヒントを得ることは大切です。自分で全部試すより、「時短」になります。
合わせて読みたい記事。
ランチェスターの法則「第二法則」(強者の戦略)

第二法則は、強者のための法則とも言われています。
どの様な法則かというと、「拳銃などの飛び道具を使った戦いの場面」に当てはまる法則です。
一度に複数の相手と戦うことができるので、数が多い方が圧倒的に有利となります。確率戦、広範戦とも呼ばれます。
具体的な数式を使った詳しい解説は後々するのですが、簡単な数式っぽいものを挙げると、
この式に近似します。^2は2乗を表します。
つまり、第一法則が適用される「一騎打ちの蓄積である戦闘」(近距離戦)よりも、「一度に複数の相手を攻撃可能な戦闘」(遠距離戦)の方が、「兵士の数」が多い方が圧倒的に有利となる。ことを意味します。
第二法則はマーケティングにどう活かす?
マーケティングに第二法則のどこを活かすか?というと、儲かりそうな新製品を発見したらそれを「模倣する」という戦略が強いです。
M&Aなどで企業ごと買収してもOKですし、技術的に可能ならさらに「上位互換」の製品を大企業の資本を使って市場に投入していくことが可能です。
それにより、幅広い製品をスピーディーに流通させて、「第一法則を使った戦い方をさせない」というのが良いと思います。
追随ですね。「ミート戦略」とも呼ばれます。
ランチェスターの法則の歴史

ランチェスターの法則のは、フレデリック・ウィリアム・ランチェスター(Frederick William Lanchester)さんが、1916年に書いた本「Aircraft in Warfare The dawn of the fourth arm.」によって提唱したのがはじまりです。
もともと、イギリスの自動車工学・航空工学のエンジニアでした。
先進的な自動車を作って、それを販売するなども行っていたそうです。
それが日本でマーケティングに応用されました。
それが「ランチェスター戦略」です。
具体的には、田岡信夫氏がランチェスターの法則を研究し、企業の経営戦略へと体系化しました。

ランチェスターの法則について具体的に数式を用いて解説

ランチェスターの法則について具体的に数式を出して解説します。
よりイメージが湧きやすくなると思うのでっ。
第一法則を数式で表す
式で表すと、
x = -at
y = -bt
と表せます。
xはXチームの残りの人数。aは武器性能を表す定数。tは経過時間。
yはYチームの残りの人数。bは武器性能を表す定数で。tは経過時間です。
またこの式から
t(x) = x0-αt
t(y) = y0-βt
↑①
x0,y0はXチーム、Yチームの人数。t(x),t(y)は経過時間tにおける残りの人数。
ここからtを消去すると、
t(x)-x0 = -αt
(x0-t(x))/α = t -②
と、
t(y)-y0 = -βt
(y0-t(y))/β = t -③
②,③から、
x0-x = α/β (y0-y) ④
この様な式が導けます。t(x),t(y)は、x,yに置き換えています。
α/βは、武器性能比です。
x0 = 5, y0 = 7 とします。
α = 1, β = 2 (武器性能)
つまり初期の人数はY軍の方が多いが、武器性能はX軍の方が強い。
それを図に表すと、下記の様に、なります。
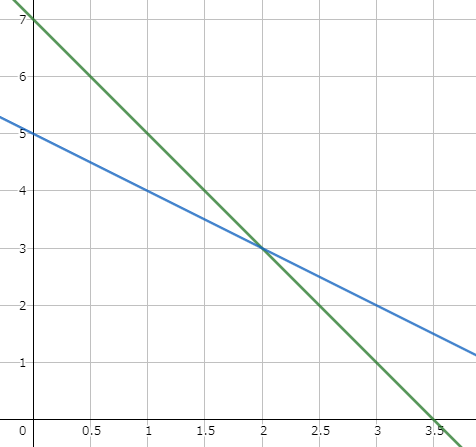
上記の図と式からから分かること
- 初期の人数では負けていても、武器性能で上回れば勝つことが可能。
- 武器性能比率が同じでも、武器性能によって全滅するまでの時間が異なる。
- お互いに一定の割合で兵士が減少する。
④より、終戦後、X軍の生き残る兵士の人数は、
5 – x = 1 / 2 (7 – 0)
x = 1.5
よって、1.5人が生存する計算になります。
近似なので、大体この人数ってことですね。予測ができます。
また、(α,β) = (1,2) , (α,β) = (2,4)
だと、武器性能比率は等しいので、生き残る兵士の人数は同じだが、
①より、戦闘にかかる時間が異なることが分かります。
第二法則を数式で表す
上記の第一法則の様に式を導くと、
(x0)^2 – x^2 = α / β ((y0)^2 – y^2)
となり、
x=5, y=7,α=1,β=3とすると、
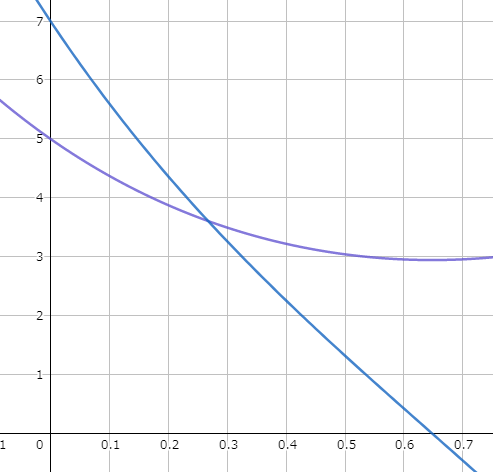
となります。
上記の図と式からから分かること
- 初期の人数では負けていても、武器性能で上回れば勝つことが可能。
- 武器性能比率が同じでも、武器性能によって全滅するまでの時間が異なる。
- Xは武器効率を1上げただけで、1.5人生存者が増える
- 最後の方はXの兵士の人数があまり減っていない。
上の2つは、一時法則と同じで、
最後の、「最後の方はXの兵士の人数があまり減っていない。」のところの
兵士の人数の差が大きいときは、「圧倒的な差がつく」ことが図からもイメージできます。
まとめ
最後まで読んでくれて、ありがとうございます!
今回の記事の内容が、何かの役に立てば幸いです!

ではっ。